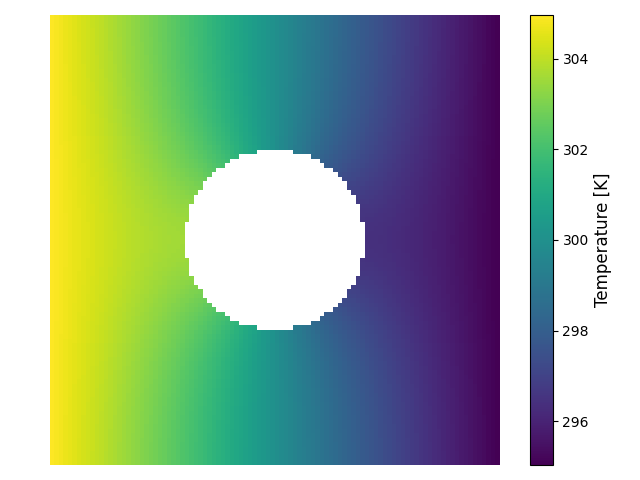Thermal Radiation

Thermal Radiation#

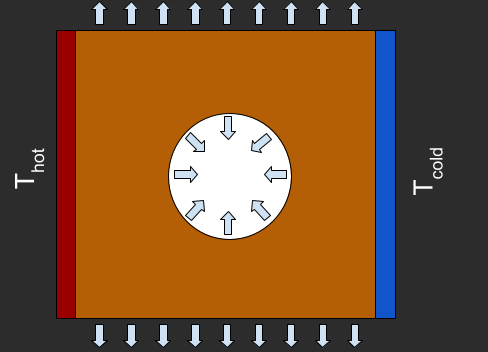
In this example, we compute the thermal losses to radiation for a porous system

animation

The key steps in the code below are:

  • The simulation domain is created using a mask, which creates the pore. To this end, we first create a Geometry2D object from which we obtain the indices of the volumes inside the pore; then, the domain is created by including these indices via a mask in a new Geometry2D object.

  • Nonlinear transport is obtained by setting mode=nonlinear in the Fourier object.

  • When creating the BoundaryConditions object, we set the default flux as given by the Stefan-Boltzmann law, which describes thermal radiation. The default is applied to all boundaries, except for regions where explicit boundary conditions are applied.

from matinverse import Geometry2D,BoundaryConditions,Fourier
from matinverse import Plot2D
from jax import numpy as jnp


L      = 0.1     # Size of the domain [m]
T0     = 300     # Base temperature [K]
DeltaT = 10      # Applied temperature [K]
sigma  = 5.67e-8 # Stefan-Boltzmann constant [W/m^2/K^4]
kappa  = 100     # Thermal conductivity [W/m/K]


size = [L,L]
N = 100
grid = [N,N]

geo = Geometry2D(grid,size)

mask = jnp.linalg.norm(geo.centroids,axis=1)>L/5

geo = Geometry2D(grid,size,mask=mask)

bcs = BoundaryConditions(geo,default_flux=lambda batch, x, t, Tb: sigma*(Tb**4-T0**4))
inds_left = bcs.temperature(lambda p: jnp.isclose(p[0], -size[0]/2), lambda batch, x, t: T0+DeltaT/2)
inds_right = bcs.temperature(lambda p: jnp.isclose(p[0],  size[0]/2), lambda batch, x, t: T0-DeltaT/2)

out,stats = Fourier(geo,boundary_conditions=bcs,\
              thermal_conductivity = lambda batch, space, temp, t: kappa*jnp.eye(2),\
              X0 = T0*jnp.ones(geo.nDOFs),\
              mode='nonlinear')


P_left = out['P_boundary'][inds_left].sum()
P_right = out['P_boundary'][inds_right].sum()
P_loss = -(P_left + P_right)
print(f'Input Power: {-P_left:.3E} W')
print(f'Output Power: {P_right:.3E} W')
print(f'Power Loss: {P_loss:.3E} W')
print(f'Converged in: {stats['num_steps']} steps')

Plot2D(out['T'],geo,design_mask=mask,cmap='viridis')

Input Power: 7.721E+02 W/m
Output Power: 7.721E+02 W/m
Power Loss: 8.629E-02 W/m
Converged in: 3 steps
animation